TÉMACSOMAGOK
Fizika
Az óra nyolc, XVII–XX. századi protestáns tudós pályáját és munkásságának legkiemelkedőbb eredményeit mutatja be, egyben azt is szemléltetve, hogy az ismeretek bővülésével hogyan jutunk el a polihisztoroktól az egy-egy szakterületre specializálódott kutatókig.
A gyakorlati ismeretszerzésre, kísérletezésre épülő óra célja, hogy a tanulók – megfigyeléseiket összekapcsolva korábbi ismereteikkel – megismerkedjenek az egyenletesen változó körmozgás szögjellemzőivel és a tehetetlenségi nyomaték jelenségével.
Az óra célja a perdület fogalmának és megmaradási törvényének feldolgozása, a tehetetlenségi nyomaték és a szögsebesség közti fordított arányosság felfedeztetése kísérletekkel és gyakorlati alkalmazásokkal. A tanultak elsajátítását és az ellenőrzést tankocka-feladatok segítik.
A tanult ismeretek (a forgómozgás alapegyenlete) alkalmazása és elmélyítése az óra keretében a bibliából (Dávid és Góliát története), a sportból és a mindennapi életből vett példákon keresztül történik. Emellett a diákok feladatmegoldás és mérés útján elemzik néhány eszköz mozgását.
A digitális kompetencia fejlesztését fókuszba helyező, csoportmunkára épülő órán a diákok megtanulják a Lego-robot kezelését, elsajátítják a mérés és adatértelmezés módszertanát, grafikonokat készítenek, valamint megismerkednek a fizika technikai fejlődésre gyakorolt hatásával.
Az egyenletesen változó körmozgás kinematikai és dinamikai jellemzőinek tisztázása, az új fogalmak bevezetése tankockafeladatokon, életszerű számpéldákon keresztül történik. Az óra végén táblázatos összesítés segíti a már ismert és új fogalmak rendszerezését, összekapcsolását.
A két, egymásra épülő tanegység első óráján az inerciarendszer, a gyorsuló vonatkoztatási rendszer, valódi és nem valódi, ún. fiktív, tehetetlenségi erők tudatos használatának elsajátítása a cél, vicces és meghökkentő videók, kísérletek és LearningApps-feladatok beépítésével az órai tevékenységbe.
A tematikus órapár második egysége a földi forgó vonatkoztatási rendszerben fellépő centrifugáliserő-hatásokon kívül a földrajz tantárgyban már megismert Coriolis erővel foglalkozik. A megértést az interneten elérhető animációk, videók, valamint LearningApps-feladatok támogatják.
Az óra keretében a tanulók megismerik az általános állapotváltozás törvényét, majd a gázállapot egyenletét, végül kiszámolják a gázállandó értékét. Az állapotváltozások ismétlése és a tudás ellenőrzése tanári prezentáció és tankockafeladatok segítségével történik.
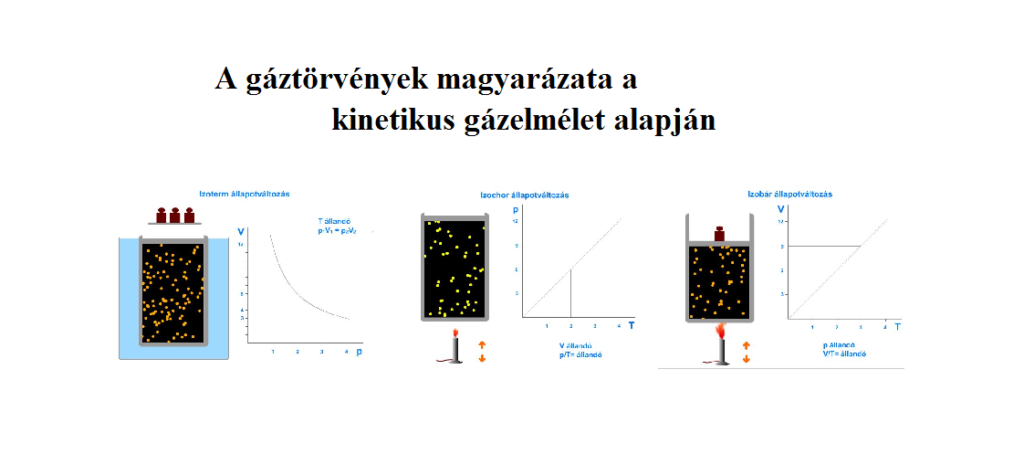
Az óra célja annak bemutatása, hogy az ideális gázmodell segítségével, a mikroszkopikus méretű gázrészecskék mozgásának leírásával eljuthatunk a gáz makroszkopikus jellemzőinek jobb megértéséhez. Az is kiderül, hogy egy jelenség megértése céljából használt modell hogyan finomítható.
Az óraterv mikroszkopikus szempontból értelmezi az állapotváltozásokat. A felhasznált animációk érthetőbbé teszik az ideális gázmodell elvont, inkább matematikai szempontból megfogható elméletét, további szemléletes képet adva a gázok viselkedéséről.
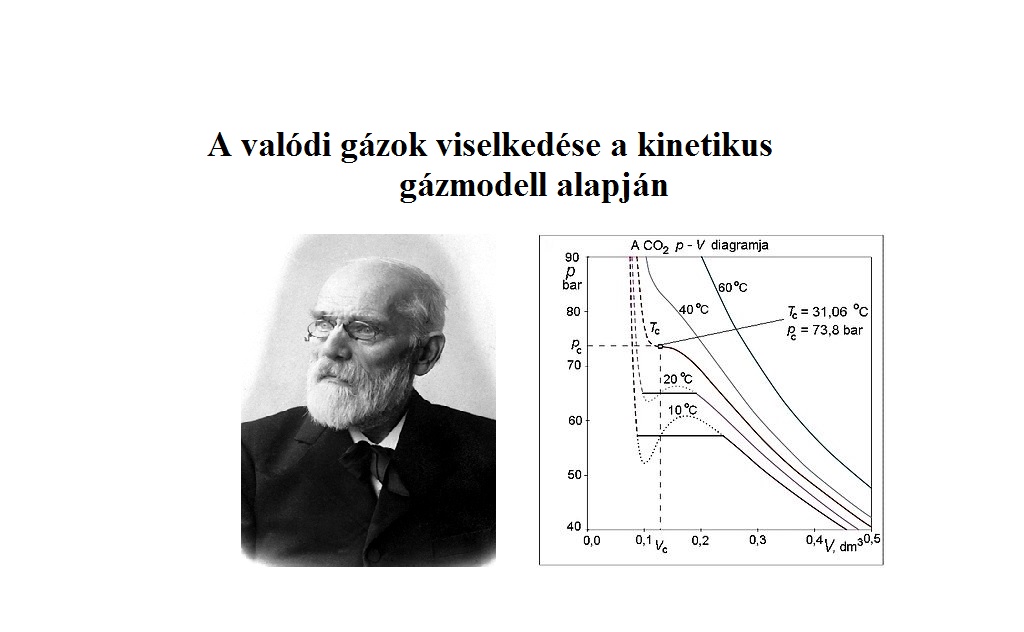
Az óra keretében értelmezzük a gázok parciális nyomását a kinetikus gázmodell alapján, és rámutatunk az ideális gázmodellünk hiányosságaira. A modell finomításának folyamatán keresztül az eredeti ideális gázmodellt is sokkal mélyebben megértjük.
A mérési hiba, illetve a becslés fogalmával ismertet meg a Lego-robottal végzett egyszerű mérés. A tanulók sebességet számolnak, grafikont készítenek és hibát elemeznek. A robot távolságmérője kapcsán szó kerül az ultrahang gyakorlati felhasználásáról is a gyógyászatban, állatvilágban.